ACM Note No.12: Dijkstra

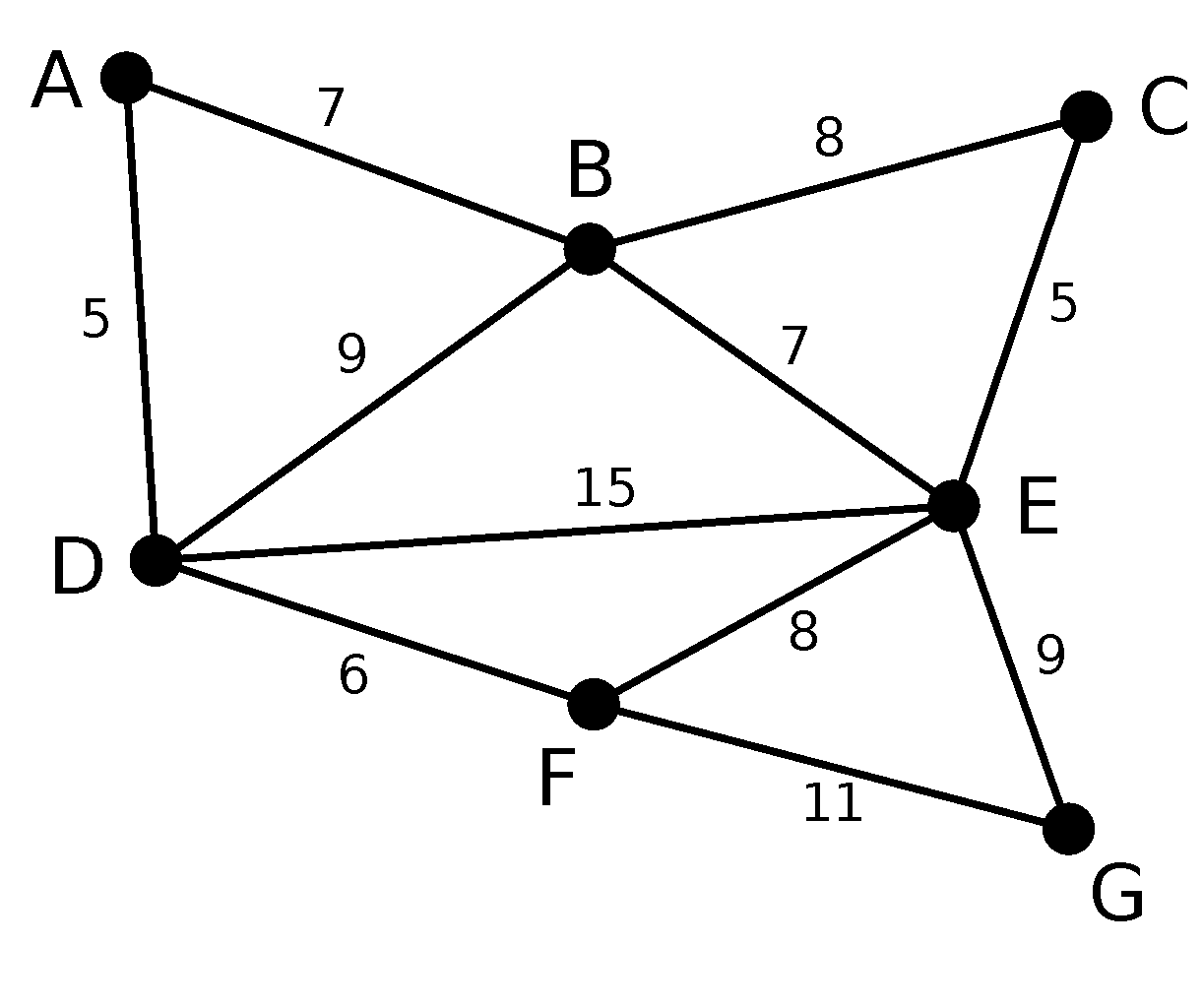
Dijkstra 算法可用于求解非负权图上的单源最短路径，在非负权图上对单个点跑一遍 Dijkstra 就可以知道该点到其他所有点的最短路径

Dijkstra 算法的核心思想是贪心：

• 如果 A -> C 的路程为 A -> B -> C 则显然当 A -> B 和 B -> C路程都最短时，A -> C的路程最短

Dijkstra 算法在使用堆优化之后的时间复杂度为O(NlogN)，具体实现参照代码

const int inf = INT_MAX;
struct edge{
    int v, w;
};
struct node{
    int dis, id;
    bool operator>(node a) const {
        return dis > a.dis;
    }
};
/**
* @param st 初始节点编号
* @param g 图的邻接表
*/
vector<int> dij(int st, vector<vector<edge>> g){
    int n = g.size();
    // 记录 st 节点到 i 节点的最短路程 dist[i]
    vector<int> dist(n);
    // 记录节点是否已经被访问
    // [已访问节点] 指的是已经计算了 [从 st 节点通过该节点到所有相邻节点的最短路程] 的节点
    vector<bool> vis(n);
    // 记录到达 v 节点的上一个节点，可以通过这个数组还原出 st 节点到某一节点的最短路径
    vector<int> fa(n);
    // 堆优化，维护未访问节点中到 st 节点距离最短的节点
    priority_queue<node, vector<node>, greater<node>> pq;
    // 将 st 点到任意一点的距离初始化为无穷远
    fill(dist.begin(), dist.end(), inf);
    
    // 初始化
    dist[st] = 0;
    pq.push({0, st});
    while(!pq.empty()){
        // 取出未访问节点中到 st 节点距离最短的节点
        int now = pq.top().id;
        pq.pop();
        if(vis[now]){
            continue;
        }

        // 访问节点 next 并将该节点标记为已访问
        vis[now] = 1;

        // 计算通过 [ st 节点到达节点 now 的最短路] 到达 [所有未访问节点的距离]
        // 如果距离比先前计算的小就进行更新
        for(auto nd : g[now]){
            int v = nd.v;
            int w = nd.w;
            if(!vis[v] && dist[now] + w < dist[v]){
                dist[v] = dist[now] + nd.w;
                // 将待访问节点更新进入优先队列
                pq.push({dist[v], v});
                // 更新到达 v 节点的上一个节点
                fa[v] = now;
            }
        }
    }
    return dist;
}