ACM Note No.11: MST
最小生成树(Minimum Spanning Tree,MST),是一个有权图删除若干边能得到的边权和最小的树
常见的求最小生成树的算法有 Prim 算法 和 Kruskal 算法
Kruskal 算法
从小到大加入边,直到所有的点连通
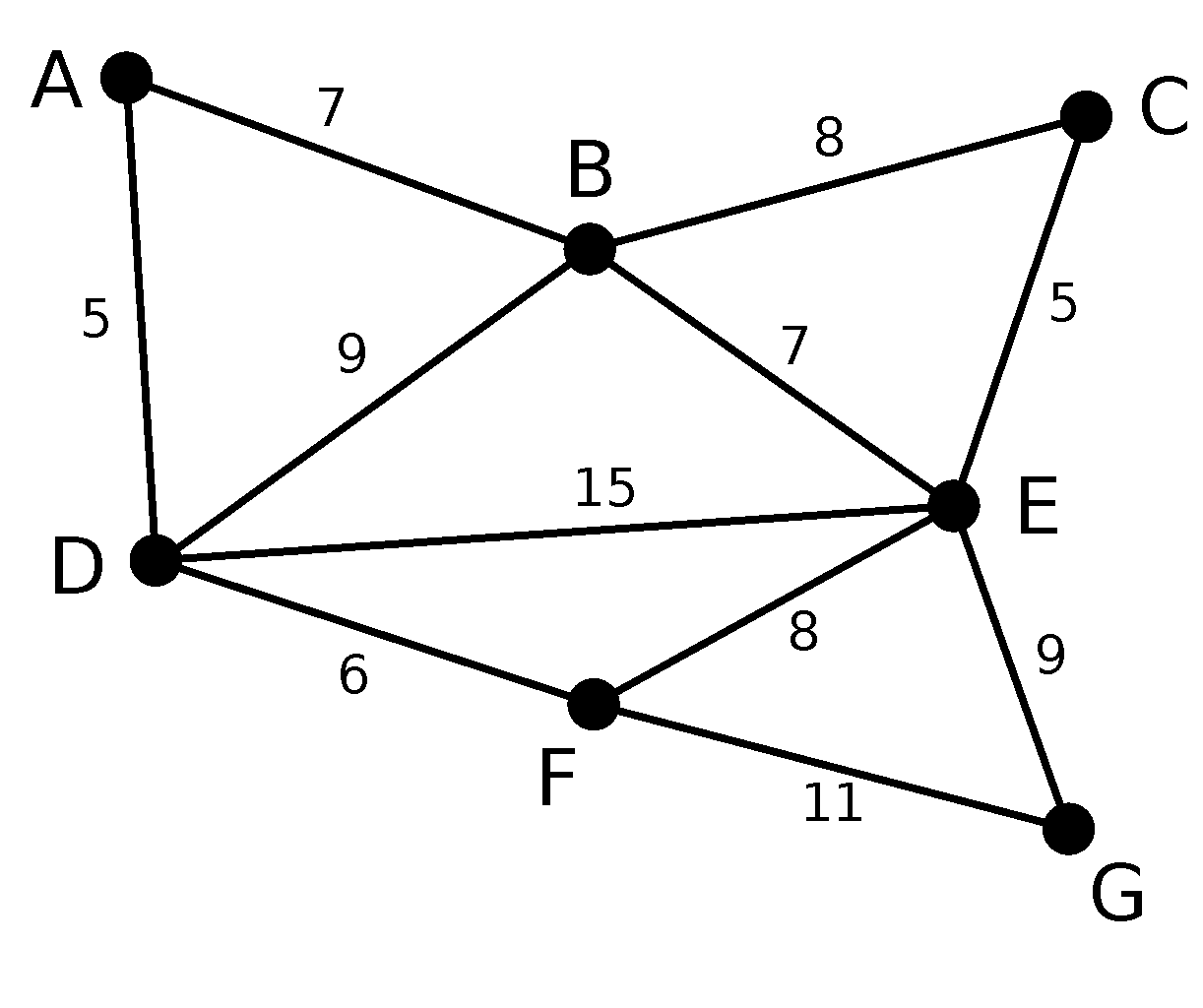
由于需要判断所有点是否连通,自然就想到可以用并查集实现
Luogu P3366
#include <bits/stdc++.h>
using namespace std;
struct node{
// x 到 y 有一条权值为 w 的边
int x, y, w;
};
// 并查集封装
struct DSU {
vector<int> fa;
int n;
DSU(int size) {
n = size;
fa = vector<int>(n);
for(int i = 0; i < n; i++){
fa[i] = i;
}
};
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void merge(int x, int y) {
fa[find(x)] = fa[find(y)];
}
bool query(int x, int y){
return find(x) == find(y);
}
};
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, m;
cin >> n >> m;
// 存储所有边
vector<node> edges;
for(int i = 0; i < m; i++){
int x, y, z;
cin >> x >> y >> z;
x--, y--;
edges.push_back({x, y, z});
}
// 对所有边从大到小排序便于后续进行贪心
sort(edges.begin(), edges.end(), [](node a, node b) -> bool {
return a.w < b.w;
});
DSU dsu(n);
vector<node> res;
for(auto nd : edges){
// 如果加入边不改变图的联通性就跳过
if(dsu.query(nd.x, nd.y)){
continue;
}
// 加入边并改变图的连通性
dsu.merge(nd.x, nd.y);
res.push_back(nd);
// 边数 == 节点数 - 1 时说明已经构成了一棵树
if(res.size() == n - 1){
break;
}
}
int sum = 0;
for(node nd : res){
sum += nd.w;
}
cout << (res.size() == n - 1 ? to_string(sum) : "orz");
return 0;
}
Prim 算法
同样是一种贪心算法,过程类似 Dijkstra
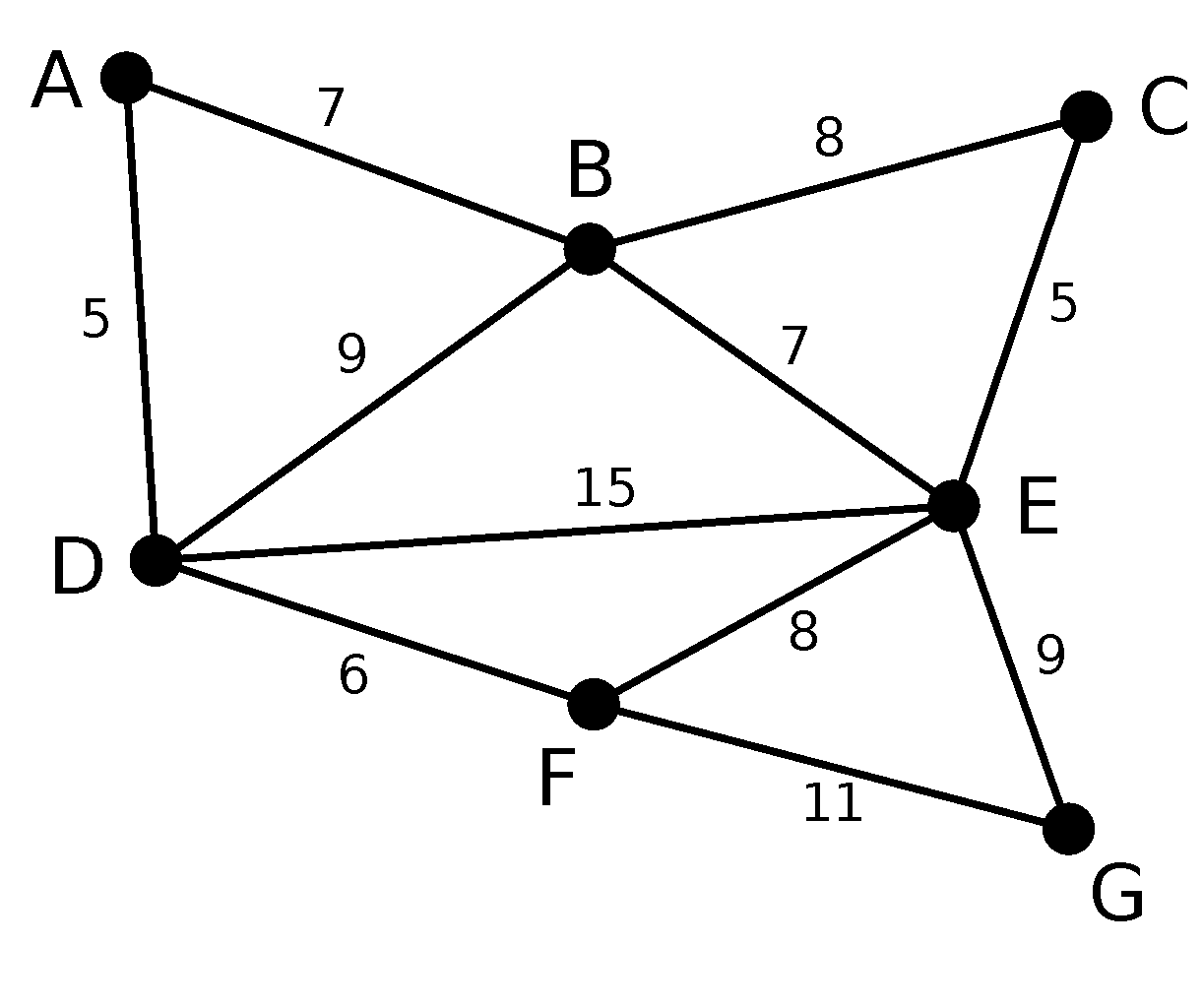
因为 Prim 算法效率一般不优于 Kruskal 算法所以一般来说使用 Kruskal 算法寻找最小生成树

Comments | NOTHING